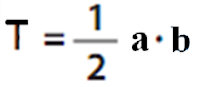Területszámítás

Részlet a Rhind-papiruszról

       A terület az egyik legrégibb matematikai fogalom. Területszámítással már az ókori egyiptomiak és görögök is foglalkoztak. A kör területének kiszámításakor a ma π-nek jelölt számot az egyiptomiak még 3,11-nak, a görögök már jobb közelítéssel 22/7-nek vették.
       Jó néhány síkbeli alakzat területét kiszámíthatjuk úgy, hogy ismert területű darabokra vágjuk őket. A terület daraboláskor összeadódik, ez egy lényeges tulajdonsága, amivel már az egyiptomiak is tisztában voltak. Területszámítási módszereikről az úgynevezett Rhind-papiruszból alkothatunk fogalmat. Az i. e. 1650-ben készült papírusz tekercs másolója azt írja, hogy az eredeti a középbirodalom idejéből (i. e. 2000-1800) származik. A papírusz 20 térfogat- és területszámítással foglalkozó feladatot és azok megoldásait tartalmazza.
        A síkbeli alakzatok területének a darabolhatóság mellett másik alapvető tulajdonsága az, hogy egy alakzatot elmozgatva a területe nem változik meg.
        A sokszögek területét úgy mérjük, hogy összehasonlítjuk a választott területegységgel.

       Téglalap területe:

       A háromszög területe egyenlő a háromszög oldala és az oldalhoz tartozó magasság szorzatának felével.

       A háromszög területe téglalappá való kiegészítéssel - az így kapott téglalap területe egyenlő a háromszög területének a kétszeresével.

       Háromszög területe átdarabolással:

        Négyszögek területe átdarabolással:

         Kör területe:

A szög fogalma, fajtái

A sík egy pontjából kiinduló két félegyenes a síkot két síkrészre, két szögre bontja. A félegyenesek a szögek szárai, a közös kezdőpont a két szög csúcsa.

A szögeket jelölhetjük a görög ábécé kisbetűivel, vagy úgy, hogy az egyik szár egy pontját, a szög csúcspontját és a másik szár egy pontját egymás után írjuk (pl. BCA∢). Mindig a középső betű jelzi a szög csúcsát.

Szögek felosztása 

 Szögpárok