Sakkmatek

A sakk egy olyan táblajáték, amelyet hagyományosan két játékos játssza egy négyzet alakú táblán. A sakktáblán 64 mező található, ebből 32 világos 32 pedig sötét színű. A mezők felváltva világos-sötét párban követik egymást. A két játékos által vezetett figurák színe szintén világos és sötét színű.

A játék célja, hogy a szabályokat betartva az egyik fél mattot adjon a másik fél királyának és ezzel megnyerje megnyerje a mérkőzést. Mindkét fél játékosának 16-16 bábú áll rendelkezésére. Hat egymástól különböző figurát különböztetünk meg - király, vezér, futó, huszár és gyalog - melyek mint formájukban, mint pedig menetmódjukban különböznek egymástól.

1256-ban az arab Ibn Kallikan foglalkozott először matematikai megközelítésben a témával. Tőle származik a híres búzaszemes feladvány. 

A sakktábla első mezőjére leteszünk egy szem búzát, majd minden következő mezőre kétszer annyit, mint az előzőre. Hány szem búzára van szükségünk összesen?

A mértani sorozat összegképlete segítségével (de anélkül is) könnyen végiggondolható, hogy a keresett szám elképesztően nagy: 2⁶⁴-1. Az emberiség a kezdetektől fogva összesen nem termelt meg ennyi búzaszemet.

Érdemes még megemlíteni Franz Nauck problémáját is: Hányféleképpen lehet 8 királynőt úgy elhelyezni egy sakktáblán, hogy semelyik kettő ne üsse egymást?

 

Íme néhány elhelyezés:

Néhány matematikai feladat  a sakktáblával kapcsolatban:

     1.  A következő két síkidom 64-64 kis négyzetből áll. Ezekből kell egy-egy sakktáblát összerakni úgy, hogy mindkettőt egyetlen vágással vágjátok két darabra. A vágásnak rácsvonal mentén kell haladnia, elkanyarodhat, de önmagába nem érhet vissza.

      2.  Lefedhető-e egy sakktábla 2x1-es dominókkal?
      3.  A sakktáblának levágjuk két átellenes sarkában lévő mezőit. Lefedhető-e ezután ez a csonka tábla 2x1-es dominókkal?
      4.  Hány téglalap van a sakktáblán?
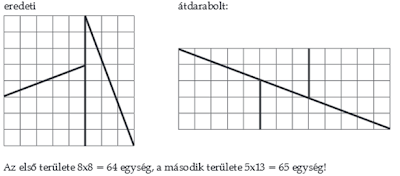
      5.  Hol a hiba?

       6. Járjuk be a sakktáblát a bástyával és a királlyal úgy, hogy a tábla bal alsó sarkából indulunk, minden mezőt egyszer érintünk, és a kezdőpontba érkezünk vissza. Keressetek minél érdekesebb megoldásokat! A bábuk csak szabályosan léphetnek!

Jó szórakozást és ismerkedést a sakktáblával!